Need help with StresStimulus? Start here.
what is Std Dev?
|
Dinesh Kakadiya Posts: 5
6/25/2011
|
Std Dev = The page response time standard deviation
how this std dev calculated ?
|
|
|
0
link
|
|
Vadim @StresStimulus Administrator Posts: 583
6/25/2011
|
Dinesh,
In short, Std Dev show how dispersed are the page responce times on multiple iterations. Below I pasted parts of Wikipedia article that explains Std Dev.
Standard deviation
From Wikipedia, the free encyclopedia
Standard deviation is a widely used measurement of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average (mean, or expected value). A low standard deviation indicates that the data points tend to be very close to the mean, whereas high standard deviation indicates that the data are spread out over a large range of values.
....................................................................
Basic examples
Consider a population consisting of the following eight values:
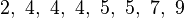
These eight data points have the mean (average) of 5:

To calculate the population standard deviation, first compute the difference of each data point from the mean, and square the result of each:

Next compute the average of these values, and take the square root:

This quantity is the population standard deviation; it is equal to the square root of the variance
....................................................................
One can find the standard deviation of an entire population in cases (such as standardized testing) where every member of a population is sampled. In cases where that cannot be done, the standard deviation s is estimated by examining a random sample taken from the population. Some estimators are given below:
With standard deviation of the sample
An estimator for s sometimes used is the standard deviation of the sample, denoted by sN and defined as follows:
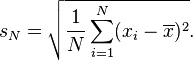
This estimator has a uniformly smaller mean squared error than the sample standard deviation (see below), and is the maximum-likelihood estimate when the population is normally distributed. But this estimator, when applied to a small or moderately sized sample, tends to be too low: it is a biased estimator.
The standard deviation of the sample is the same as the population standard deviation of a discrete random variable that can assume precisely the values from the dataset, where the probability for each value is proportional to its multiplicity in the dataset.
|
|
|
0
link
|
Copyright © 2026 Stimulus Technology